Wprowadzenie do przetwarzania obrazów

Politechnika Poznańska, Instytut Robotyki i Inteligencji Maszynowej

Ćwiczenie laboratoryjne 3: Filtracja

Powrót do spisu treści ćwiczeń laboratoryjnych

Ciekawostka - historia zdjęcia Lenna:

http://en.wikipedia.org/wiki/Lenna

Filtracja obrazów

W przetwarzaniu obrazów występują dwa główne rodzaje szumu:

• Szum detektora - wynika z dyskretnej natury stosowanych przetworników, tj. faktu, że stosowane przyrządy działają na zasadzie zliczania fotonów. Zazwyczaj przyjmuje się, że może być modelowany przez niezależny od obiektu, addytywny szum o rozkładzie normalnym z zerową wartością średnią i pewną wariancją.

• Szum “sól i pieprz” wynika głównie z błędów transmisji. Poszczególne piksele mają ustawianą albo wartość maksymalną (“sól”) albo minimalną (“pieprz”). Zakłócona jest tylko część pikseli obrazu, pozostałe pozostają bez zmian.

Operacją, która może pozwolić na usunięcie szumu z obrazu jest operacja filtracji. Filtracja jest operacją, która bierze pod uwagę otoczenie (sąsiedztwo) piksela, dla którego jest wykonywana. Wszystkie elementy w jego sąsiedztwie są przemnażane przez odpowiadające im współczynniki filtra, a suma tych wartości jest zapisywana jako zaktualizowana wartość piksela, który był filtrowany. Jest to tzw. konwolucja 2D.

Liniowe filtry wygładzające - filtr uśredniający

Najprostszym sposobem usunięcia szumu, który równomiernie oscyluje pod i nad ‘prawdziwą’ wartością funkcji obrazowej jest lokalne uśrednianie po pewnym obszarze. Uśrednianie może być realizowane przy wykorzystaniu maski prostokątnej lub kołowej, np.:

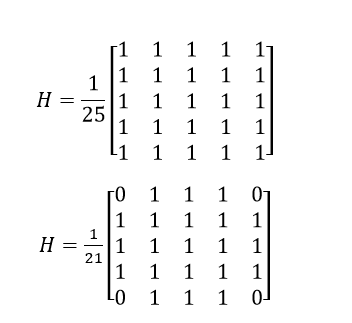
Rezultatem splotu z takim filtrem będzie obraz o mniejszym natężeniu szumu, lecz również o mniejszej ostrości.

Liniowe filtry wygładzające - filtr gaussowski

Poprawę jakości wygładzania można uzyskać poprzez zastosowanie uśredniania ważonego odległością od środka filtru. Jedną z takich metod jest filtracja wygładzającym filtrem gaussowskim. Poszczególne elementy jądra filtru o rozmiarze \(2k + 1 × 2k + 1\) są określane zgodnie ze wzorem:

\[ H(i, j)= \frac{1}{2 \pi \sigma ^ {2}} \exp - \Bigg( \frac{(i-k-1) ^ {2} + (j-k-1) ^ {2}}{2 \sigma ^ {2}} \Bigg) \]

Rezultat filtracji zależy od wybranego \(\sigma\) :

• małe odchylenie standardowe sprawi, że efekt wygładzania będzie niezauważalny - wagi oddalone od środka jądra będą niewielkie
• większe odchylenie sprawi, że wagi oddalone od środka przyjmą większe wartości, a rezultat będzie dążył do średniej z sąsiedztwa, w efekcie szum zostanie w dużej mierze zniwelowany, lecz obraz ulegnie rozmyciu
• bardzo duże odchylenie sprawi, że wiele szczegółów obrazu zostanie usuniętych razem z szumem

Nieliniowe filtry wygładzające - filtr medianowy

Podstawową wadą filtrów liniowych jest rozmywanie krawędzi na obrazie. Aby tego uniknąć konieczne jest zastosowanie filtrów nieliniowych. Jednym z takich filtrów jest filtr medianowy. Zastosowanie tego filtru polega na przypisaniu pikselowi wartości będącej medianą w pewnym sąsiedztwie. Filtr ten nadaje się szczególnie do usuwania niewielkich artefaktów (np. szumu “pieprz i sól”).

Uwaga:
W OpenCV powyższe operacje filtrowania zostały zaimplementowane pod nazwami cv2.blur(), cv2.medianBlur() oraz cv2.GaussianBlur(). Więcej informacji znajdziesz w dokumentacji: https://docs.opencv.org/5.x/d4/d13/tutorial_py_filtering.html.

💥 Zadanie do wykonania 💥

• Pobierz dwa obrazy z wprowadzonymi zakłóceniami:

  • lenna_noise.bmp

  • lenna_salt_and_pepper.bmp

• Wyświetl jeden z pobranych obrazów, a następnie korzystając z poznanych funkcji do filtracji (filtr uśredniający, filtr Gaussa, filtr medianowy) zaprezentuj ich działanie. Wyświetlić rezultat działania każdego z filtrów w osobnym oknie w celu porównania efektów filtracji.

• Dodaj trackbar umożliwiający sterowanie rozmiarem okna filtracji (wartość powinna być nieparzysta, wykorzystaj wzór na liczby nieparzyste 2n+1).

• Wykonaj filtrację na obu obrazach z zakłóceniami. Zwróć uwagę na efekty filtracji: w zależności od naniesionego szumu oraz rozmiaru okna filtracji.

Operacje morfologiczne

💥 Zadanie do wykonania 💥

Zapoznaj się z operacjami morfologicznymi: https://docs.opencv.org/5.x/d9/d61/tutorial_py_morphological_ops.html. A następnie:

• Wykorzystując program z poprzednich zajęć, który wykonywał operację progowanie binarnego, wykonaj na obrazie binarnym jedną z operacji cv2.erode lub cv2.dilate. Wyświetl w osobnych oknach obraz po samej operacji progowania, a w osobnym obraz po progowaniu i operacji morfologicznej.

• Dodaj trackbar, który umożliwia sterowanie rozmiarem maski wykorzystywanej w operacji morfologicznej. Zaobserwuj efekt jej zmiany.

• Po przetestowaniu erozji i dylacji przetestuj otwarcie i domknięcie. Zastanów się, kiedy przydatna może być operacja domknięcia, a kiedy otwarcia.

Skanowanie obrazu

OpenCV zawiera bardzo dużo gotowych, zoptymalizowanych funkcji operujących na obrazach, jednak w niektórych, stosunkowo rzadkich, przypadkach niezbędne jest operowanie bezpośrednio na obrazie i jego pikselach. Można to zrealizować korzystając z pętli for. Szerokość, wysokość oraz liczbę kanałów (dla obrazów kolorowych) można uzyskać wywołując własność shape. Następnie iterujemy po szerokości, wysokości i (ewentualnie) liczbie kanałów.

💥 Zadanie do wykonania 💥

• Wczytaj dowolny obraz w skali szarości, korzystając z pętli, przeiteruj po obrazie i co trzeci piksel w wierszu zamień na biały (wartość 255).

• Napisz program, który wykona na powyższym obrazie operację wygładzania w oknie 3x3 w krokach:

  • zsumuj wszystkie piksele z wiersza nad/pod oraz kolumny przed/po
  • podziel sumę przez liczbę pikseli (9).

  Program powinien pominąć pierwszy/ostatni wiersz oraz pierwszą/ostatnią kolumnę.

• Porównaj czas wykonywania oraz jakość działania z wbudowaną funkcją cv2.blur(src, (3, 3)).

• Porównać czas wykonania oraz jakość działania z realizacją uśredniania za pomocą funkcji cv2.filter2D.

Zadania do samodzielnej realizacji

💥 Zadanie do wykonania 💥

W powyższym zadaniu, piksele “na obramowaniu” obrazu zostały pominięte. Zapoznaj się z innymi sposobami przetwarzania pikseli na jego brzegach: https://docs.opencv.org/5.x/d2/de8/group__core__array.html#ga209f2f4869e304c82d07739337eae7c5

💥 Zadanie do wykonania 💥

Napisz funkcję implementującą filtr Kuwahary (do obliczeń dla wygody wykorzystać można funkcję meanStdDev).

Czym jest filtr Kuwahary? Jest on innym przykładem filtru zachowującego krawędzie. Może być on określony dla różnych kształtów okna, jednak najczęściej przyjmuje się okno kwadratowe o długości boku równej \(2L + 1\) gdzie \(L\) jest liczbą całkowitą. Okno jest dzielone na 4 części jak na rysunku:

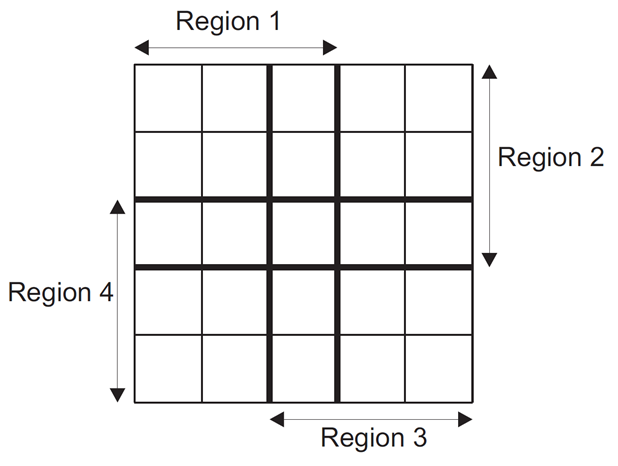
Dla każdej części określana jest wariancja i wartość średnia. Pikselowi bazowemu (środkowemu) przypisywana jest wartość średnia z obszaru o najmniejszej wariancji.